Table des matières
Ateliers Processing de l'OA
Sketch 01

L'idée de ce premier atelier était d'implémenter un algorithme d'art contemporain proposé par Sol LeWitt.
L'idée a été trouvée sur le site de Pol Guezennec
Bon, c'est vrai qu'on commence sur des chapeaux de roues, avec l'utilisation des boucles `for` et des listes, mais j'essaierai de garder un niveau de complexité constant, afin de ne pas pénaliser ceux·elles qui raccrocheraient le wagon en cours d'année. Si ce premier sketch vous semble compliqué (et il l'est lorsqu'on débute), les suivants devraient vous paraître de plus en plus simples, à force de répétition.
FloatList liste_x = new FloatList(); FloatList liste_y = new FloatList(); void setup() { // Dans la fonction setup on mets les instructions qui n'ont // besoin d'être exécutés qu'une seule fois, au démarrage size(500, 500); background(255); for (int i = 0; i < 50; i = i+1) { liste_x.append(random(width)); liste_y.append(random(height)); } } void draw() { // La fonction draw s'exécute à chaque rafraichissement de l'écran (60 fois/secondes par défaut) stroke(random(255), random(255), random(255)); // Couleur des contours strokeWeight(0.1); // Épaisseur des countours int i0 = int(random(50)); int i1 = int(random(50)); line(liste_x.get(i0), liste_y.get(i0), liste_x.get(i1), liste_y.get(i1)); }
Sketch 02
Ici nous abordons les boucles “for” pour répéter un bloc d'instructions. Nous imbriquons deux boucles “for” pour créer la grille sur deux dimensions.

int diametre = 40; // Diamètre des cercles void setup() { size(500, 500); noStroke(); // Désactive le countour des formes fill(#FFE990); // Couleur de remplissage des cercles } void draw() { background(#90A5FF); // On repeint le fond for (int j = 0; j < height; j += diametre) { // A chaque tour de la boucle externe on descend d'une ligne for (int i = 0; i < width; i += diametre) { // A chaque tour de la boucle interne on décalle d'une colonne int posx = i + diametre/2; int posy = j + diametre/2; // On calcule la distance entre le centre de chaque cercle et le curseur de la souris float d = dist(posx, posy, mouseX, mouseY); circle(posx, posy, d * 0.18); } } }
Sketch 03
Pour sortir de la monotonie des lignes droites, essayons-nous aux courbes !
Première forme
Ce sketch est interactif. Cliquez dans la fenêtre pour rajouter des points d'ancrages à la courbe.
ArrayList<PVector> points = new ArrayList(); void setup() { size(500, 500); noFill(); } void draw() { background(255); beginShape(); curveVertex(0, 0); // On rajoute un premier point de contrôle aux mêmes coordonnées que le premier point d'ancrage de la courbe curveVertex(0, 0); for (PVector p : points) { p.x = p.x + random(-1,1)*2; // On modifie légèrement les coordonnées de chaque points pour l'effet de vibration p.y = p.y + random(-1,1)*2; curveVertex(p.x, p.y); } curveVertex(width, height); curveVertex(width, height); // Un dernier point de contrôle pour terminer la courbe endShape(); for (PVector p : points) { circle(p.x, p.y, 10); } } void mousePressed() { points.add(new PVector(mouseX, mouseY)); // Chaque clique ajoute un nouveau points aux coordonnées du curseur de la souris }
Seconde forme
Dans le style de l'harmonographe.
ArrayList<PVector> list = new ArrayList(); void setup() { size(500, 500); background(255); strokeWeight(0.2); } void draw() { float x = 200 * cos(millis() * 0.005); float y = 200 * sin(millis() * 0.003); fill(0, 0); //background(255); beginShape(); curveVertex(width*0.5, 50); curveVertex(width*0.5, 50); curveVertex(width*0.5 + x, height*0.5 + y); curveVertex(width*0.5, height-50); curveVertex(width*0.5, height-50); endShape(); } void mouseClicked() { list.add(new PVector(mouseX, mouseY)); }
Sketch 04 : Spirale Polaire
Je ne m'attendais pas à voir venir beaucoup de monde le 4 Janvier, pour le premier atelier Processing de cette nouvelle année. Puisqu'à l'heure prévue il n'y avait qu'Alex et moi, j'ai voulu proposer quelque chose d'un peu plus complexe que d'habitude. L'idée était de créer des spirales denses, à la façon des sillons de disques vinyle.
La méthode la plus “simple” (à condition de connaître un peu de trigonométrie) est de faire usage des coordonnées polaires. Tout à fait approprié dans les conditions arctiques que nous avons actuellement à la Baleine. Ne vous laissez pas intimider par ces mathématiques froides et souvenez-vous que l'essentiel est de dessiner des jolis trucs à l'écran.
Le mini cours de trigo sur les coordonnées polaires

Pour décrire la position d'un point dans un espace en deux dimensions, on a l'habite d'utiliser les coordonnées cartésiennes (x,y) où x représente la distance depuis l'origine sur l'axe horizontal et y la distance sur l'axe vertical.
Sur la figure précédente, l'origine est en bas à gauche du repère. Dans Processing l'origine du repère cartésien se trouve en haut à gauche. Normalement là je ne vous apprend rien.
Une autre façon pour décrire la position d'un point est par les coordonnées polaires (φ,θ), ou φ est la distance euclidienne à vol d'oiseau entre l'origine et notre point, et θ est l'angle entre la droite origine-point et l'axe horizontal.
Si on imagine un cercle centré sur l'origine du repère et traversant le point p, alors la distance φ est égal au rayon de ce cercle. D'ailleurs les lettres grecs sont un peu pénibles à taper au clavier alors on utilisera plutôt les lettres (r,a) pour nos coordonnées polaires.
On peut aussi imaginer le cadran d'un horloge avec les chiffres des heures situés sur le périmètre du cercle. Dans ce cas toutes les heures on la même coordonnée r (elles sont toutes à la même distance du centre, correspondante au rayon du cadran) mais elles ont toutes une coordonnée a (angle) différente. L'angle 0 (zéro) se situerait à 3 heures. “12h” aurait l'angle +90° et “9h” aurait l'angle -90°. Si on fait un tour complet (360°) on revient sur le même point, donc les coordonnées (r, 10°) et (r, 370°) décrivent exactement la même position.
Bon alors il y a une subtilité : en trigonométrie on ne compte pas les angles en degrés comme tout le monde, mais en radians, qui permettent de donner un angle en fraction de PI. Un tour de cercle complet (360°) fait 2×PI radians. Vous l'aurez deviné, un demi tour de cercle (180°) fait donc PI radians. Sur notre cadran d'horloge, “12h” est à l'angle PI/2 radians et “9h” est à l'angle -PI/2 radians (ou bien (3/4)×PI, si on tourne toujours dans le même sens). C'est le fameux cercle trigonométrique, où l'angle croît dans le sens anti-horaire.
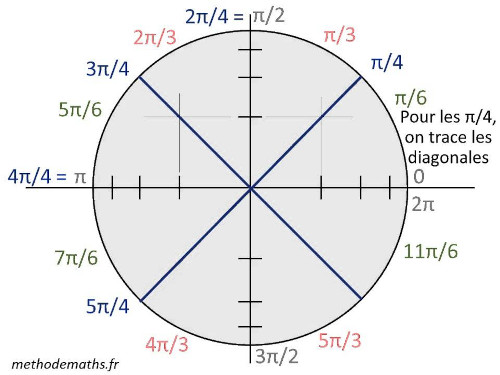
J'espère que vous n'avez pas la tête qui tourne trop, car il y encore une autre subtilité. Vous vous souvenez peut-être que dans Processing (et beaucoup d'autres environnement de programmation), l'axe y est inversé (y grandit de haut en bas) ? Et bien c'est la même chose pour le sens de rotation. Sous processing, l'angle grandit dans le sens horaire, contrairement aux conventions mathématiques !
Enfin, connaissant les coordonnées polaires un point, on peut calculer ses coordonnées cartésiennes (essentiel pour se situer sur une grille de pixels, comme celle de notre fenêtre graphique) en appliquant les formules suivantes :
x = r × cos(a) et y = r × sin(a), où x et y sont nos coordonnées cartésiennes et r et a sont nos coordonnées polaires (avec a en radian bien entendu). Les fonctions cos() et sin() se trouvent comme telles dans Processing, et on a même les fonctions radians() pour convertir les angles en degrés vers radians, et degrees() pour convertir les angles en radians vers degrés.
Ouf ! On va enfin pouvoir programmer !
Première forme

void setup() { size(500, 500); } void draw() { background(255); translate(width/2, height/2); // Pour déplacer l'origine au milieu de la fenêtre // On initialise les variables dont on aura besoin PVector p1 = new PVector(); // Un premier point PVector p2 = new PVector(); // Un deuxième point float angle = 0.0; // l'angle actuel (en radians) float radius = 0.0; // le rayon actuel while (radius < width*0.5) { p1.set(radius * cos(angle), radius * sin(angle)); // On définit un premier point aux coordonnées actuelles angle += 0.2f; // On augmente légèrement l'angle (en radians) radius += 0.3f; // et le rayon p2.set(radius * cos(angle), radius * sin(angle)); // On définit le deuxième point aux nouvelles coordonnées line(p1.x, p1.y, p2.x, p2.y); // On trace une ligne entre nos deux points // Et on recommence ! (tant que le rayon est inférieur à un certain seuil) } } void keyPressed() { // Pratique pour exporter des captures d'écran // (elles seront placés dans le sous-dossier "data" du sketch) // On peut ouvrir le dossier du sketch avec le raccourci Ctrl+K if (key == 'p') { saveFrame("####.png"); } }
Seconde forme (en 3D)
Je suis resté longtemps à progra-dessiner en 2D avant d'oser franchir le pas de la 3D avec Processing. Et pourtant il suffit de pas grand chose pour rajouter une toute nouvelle dimension à vos créations. Avec la librairie PeasyCam vous pourrez naviguer très facilement à l'aide de la souris pour admirer vos œuvres sous tous les angles, même les dessins plats.
Pour installer la librairie PeasyCam, assurez-vous d'être relié à Internet puis cliquez sur le menu “Sketch” > “Importer une librairie…” > “Manage librairies” (chez moi c'est en anglais). Écrivez “peasycam” dans le champ de recherche et enfin cliquez sur le bouton “Install”.

import peasy.*; // On importe la librairie peasyCam PeasyCam cam; // Cette variable va contenir les infos de notre caméra void setup() { size(800, 800, P3D); // On choisit le moteur de rendu "P3D" pour la 3D cam = new PeasyCam(this, 400); // On crée la caméra } void draw() { background(255); PVector p1 = new PVector(); PVector p2 = new PVector(); float angle = 0.0; float radius = 0.0; while (radius < width*0.5) { p1.set(radius * cos(angle), radius * sin(angle)); angle += 0.1f; radius += 0.02f; p2.set(radius * cos(angle), radius * sin(angle)); float seg_angle = sin(2 * atan2(p2.y-p1.y, p2.x-p1.x)); // Un peu de magie trigonométrique stroke(seg_angle*200); // Qui colore les segments en fonction de l'angle que forment les deux points line(p1.x, p1.y, p2.x, p2.y); } }
Forme ultime
Voilà ce que ça peut donner, avec une bonne dose d'obstination de persévérance et de caféine trigonométrie.
Le texte pour l'étiquette a été fait avec Inkscape (le fichier, nommé “label.png”, doit être placé dans le répertoire du sketch).

import peasy.*; PeasyCam cam; float LABEL_RADIUS = 130.0f; float RECORD_RADIUS = 400f; PVector p1 = new PVector(); PVector p2 = new PVector(); float rec_rot = 0.0f; float rot_speed = 0.02f; PImage label; void setup() { size(500, 500, P3D); //fullScreen(P3D); hint(DISABLE_DEPTH_TEST); // Pour éviter les problèmes de superposition lorsqu'on dessine plusieurs objets sur le même plan en 3D cam = new PeasyCam(this, 400); label = loadImage("label.png"); } void draw() { background(255); // Dessiner les sillons du vinyle fill(0); noStroke(); circle(0, 0, 2 * RECORD_RADIUS); strokeWeight(1.4); float angle = rec_rot; float radius = LABEL_RADIUS; while (radius < LABEL_RADIUS + 34) { p1.set(radius * cos(angle), radius * sin(angle)); angle += 0.05f; radius += 0.14f; p2.set(radius * cos(angle), radius * sin(angle)); float seg_angle = 1.02 * sin(2 * atan2(p2.y-p1.y, p2.x-p1.x)); seg_angle *= seg_angle * seg_angle; seg_angle += 0.5 * sin(2 * atan2(p2.y-p1.y, p2.x-p1.x) + PI); seg_angle += random(0.2f); seg_angle *= 230; stroke(seg_angle * 0.8, seg_angle*0.8, seg_angle); line(p1.x, p1.y, p2.x, p2.y); } while (radius < RECORD_RADIUS - 14) { p1.set(radius * cos(angle), radius * sin(angle)); angle += 0.03f; radius += 0.005f; p2.set(radius * cos(angle), radius * sin(angle)); float seg_angle = 1.02 * sin(2 * atan2(p2.y-p1.y, p2.x-p1.x)); seg_angle *= seg_angle * seg_angle; seg_angle *= seg_angle * seg_angle; seg_angle += 0.5 * sin(2 * atan2(p2.y-p1.y, p2.x-p1.x) + PI); seg_angle += random(0.1f); seg_angle *= 230; stroke(seg_angle * 0.8, seg_angle*0.8, seg_angle); line(p1.x, p1.y, p2.x, p2.y); } // L'étiquette centrale noStroke(); fill(255, 255, 0); circle(0, 0, LABEL_RADIUS * 2); rotate(rec_rot); image(label, -label.width*0.5, -label.height*0.5); // Le trou central fill(255); circle(0, 0, 20); rec_rot += rot_speed; if (rec_rot > TWO_PI) { rec_rot -= TWO_PI; } }

Sketch 05 : Étoile des neiges...
Encore un truc de saison, saupoudré de kitshitude, avec cette ode à l'hiver : nous allons faire tomber de flocons. Une façon d'aborder les particules et de s'émerveiller devant son écran.
On commence par trouver une belle image de flocon sur internet (je ne sais plus d'où je l'ai sorties donc excusez l'absence de source et de licence…)
La seconde image a été dérivée de la première en y appliquant un flou gaussien dans le logiciel Gimp.


PImage fl_flou; PImage fl_moyen; PImage fl_petit; ArrayList<PVector> flocons_pos = new ArrayList(); // Liste qui contiendra la position de chaque flocon ArrayList<PImage> flocons_img = new ArrayList(); // Liste qui contiendra l'image de chaque flocon void setup() { size(800, 600); fl_flou = loadImage("snowflake_flou.png"); fl_moyen = loadImage("snowflake_400.png"); fl_moyen.resize(100, 0); // On redimensionne l'image à 100 pixels de largeur, fl_petit = fl_moyen.copy(); fl_petit.resize(50, 0); // le second argument '0' permet de garder la même proportion pour la hauteur for (int i=0; i<30; i++) { // On crée 30 petits flocons flocons_img.add(fl_petit); flocons_pos.add(new PVector(random(width), random(height))); } for (int i=0; i<10; i++) { // 10 flocons moyens flocons_img.add(fl_moyen); flocons_pos.add(new PVector(random(width), random(height))); } for (int i=0; i<4; i++) { // et 4 gros flocons flocons_img.add(fl_flou); flocons_pos.add(new PVector(random(width), random(height))); } } void draw() { background(255); for (int i=0; i<flocons_img.size(); i++) { PImage img = flocons_img.get(i); PVector pos = flocons_pos.get(i); pos.y += img.width * 0.01; // Le floncon tombe à une vitesse proportionelle à sa taille pos.x += random(-1, 1); pos.y += random(-1, 1); pos.z += random(0, 1) * 0.1; // Rotation du flocon if (pos.y > height + img.height/2) { pos.y = -img.height/2; // On replace le flocon au dessus de la fenêtre pos.x = random(width) - img.width/2; // Avec une position horizontale aléatoire } // Les instructions suivantes permettent de faire une rotation et une translation du flocon push(); translate(pos.x, pos.y); rotate(pos.z); image(img, -img.width*0.5, -img.height*0.5); pop(); } }
Seconde forme : Vitesse et accélération
Pour le moment l'animation des flocons est saccadée puisque qu'ils sautent d'une position à une autre (à une distance aléatoire). Ça donne un effet stop-motion assez sympa, mais si on veut avoir des mouvements plus naturels il va falloir procéder d'une autre façon : en utilisant un variable de vitesse.
PImage fl_flou; PImage fl_moyen; PImage fl_petit; ArrayList<PVector> flocons_pos = new ArrayList(); ArrayList<PImage> flocons_img = new ArrayList(); ArrayList<PVector> flocons_vel = new ArrayList(); // Liste qui contiendra la vitesse (linéaire et angulaire) de chaque flocon void setup() { size(500, 500); fl_flou = loadImage("snowflake_flou.png"); fl_moyen = loadImage("snowflake_400.png"); fl_moyen.resize(100, 0); fl_petit = fl_moyen.copy(); fl_petit.resize(50, 0); for (int i=0; i<30; i++) { flocons_img.add(fl_petit); flocons_pos.add(new PVector(random(width), random(height))); } for (int i=0; i<10; i++) { flocons_img.add(fl_moyen); flocons_pos.add(new PVector(random(width), random(height))); } for (int i=0; i<4; i++) { flocons_img.add(fl_flou); flocons_pos.add(new PVector(random(width), random(height))); } // Donne une vitesse aléatoire (la troisième valeur étant la vitesse de rotation) à chaque flocon for (int i=0; i<flocons_img.size(); i++) { flocons_vel.add(new PVector( random(-1, 1) * 0.01, random(-1, 1) * 0.01, random(-1, 1) * 0.1 )); } } void draw() { background(255); for (int i=0; i<flocons_img.size(); i++) { PImage img = flocons_img.get(i); PVector pos = flocons_pos.get(i); PVector vel = flocons_vel.get(i); // On récupère la vitesse de ce flocon // On ajoute une accélération aléatoire à la vitesse vel.x += random(-1, 1) * 0.004; vel.y += random(-1, 1) * 0.002; vel.z += random(-1, 1) * 0.001; pos.y += img.width * (vel.y + 0.04); // La position augmente en fonction de la vitesse pos.x += vel.x; pos.z += vel.z; if (pos.y > height + img.height/2) { pos.y = -img.height/2; pos.x = random(width) - img.width/2; vel.y = 0; } // Les instructions suivantes permettent de faire une rotation et une translation du flocon push(); translate(pos.x, pos.y); rotate(pos.z); image(img, -img.width*0.5, -img.height*0.5); pop(); } }

Sketch 06 : Pluie
On continue de suivre le fil des saisons avec une idée proposée par Martin et inspirée par un sketch, Impluvium de Pol Guezennec.
La particularité de cet exercice (et sa complexité) tient dans le fait qu'il y a deux états à l'animation : le premier lorsque la goutte tombe verticalement, le second lorsque 3 ondes croissent jusqu'à atteindre chacun leur taille maximale.
Puisqu'il n'y a que ces deux états on pourra utiliser une variable etat de type boolean (valeur binaire true ou false) pour définir l'état actuel de notre euh… élément aqueux.
L' etat passera de false (goutte tombante) à true (onde croissante) lorsque la goutte sera tombée d'une hauteur supérieure à la composante y de la variable pg. pg est un vecteur à deux composantes (x et y) qui définit à la fois le point de départ (sur l'axe horizontal) et le point d'arrivée (sur l'axe vertical) de notre goutte. Les valeurs de pg seront réinitialisées au hasard à chaque nouveau cycle pour ajouter un peu de variété à l'animation.
L'illusion n'est pas parfaite car la goutte disparaît instantanément après impact pour laisser place aux ondes. Si on était soucieux du réalisme on tronquerait progressivement la partie inférieur de la goutte qui est au-delà du point d'impact mais bon… L'animation est suffisamment rapide pour qu'on y voit que du feu !

// Variables de l'état "goutte" float vitesse_goutte = 30; // Vitesse verticale (en pixel/frame) float taille_goutte = 70; float inclinaison = 20; // Décallage horizontal (en pixels) entre le haut et le bas de la goutte PVector pg = new PVector(random(500), 370); // Contient la coordonnée horizontale de la goutte (x) // Et la coordonnée verticale du point d'impact final (y) PVector p1 = new PVector(pg.x, -taille_goutte); // Point supérieur de la goutte PVector p2 = new PVector(pg.x + inclinaison, 0); // Point inférieur de la goutte // Variables de l'état "onde" float vitesse_onde = 3; // Vitesse de croissance des ondes (en pixel/frame) float decalage_onde = 40; // Décallage entre chaque onde (en pixels) float taille = 0.0; // Taille de la première onde, à chaque instant float taille2 = -1 * decalage_onde; // Taille de la deuxième onde, à chaque instant float taille3 = -2 * decalage_onde; // Taille de la troisième onde, à chaque instant float taille_max = 150; float ratio = 2.5; // Ratio entre la largeur et la hauteur de l'onde boolean etat = false; // État goutte si "true, état onde si "false" void setup() { size(500, 500); stroke(#9D62FF); strokeWeight(2); noFill(); } void draw() { background(255); if (etat == false) { // Goutte d'eau p1.y += vitesse_goutte; // La goutte descend (verticalement) p2.y += vitesse_goutte; p1.x += vitesse_goutte * inclinaison / taille_goutte; // La goutte se décalle en fct de son inclinaison p2.x += vitesse_goutte * inclinaison / taille_goutte; line(p1.x, p1.y, p2.x, p2.y); if (p2.y > pg.y) { etat = true; pg.x = p2.x; } } else { // Ondes taille = taille + vitesse_onde; taille2 = taille2 + vitesse_onde; taille3 = taille3 + vitesse_onde; if (taille > 0 && taille < taille_max) ellipse(pg.x, pg.y, ratio * taille, taille); if (taille2 > 0 && taille2 < taille_max) ellipse(pg.x, pg.y, ratio * taille2, taille2); if (taille3 > 0) ellipse(pg.x, pg.y, ratio * taille3, taille3); if (taille3 > taille_max) { taille = 0.0; taille2 = -1 * decalage_onde; taille3 = -2 * decalage_onde; etat = false; pg = new PVector(random(0, 500), random(200, 400)); p1 = new PVector(pg.x, -taille_goutte); p2 = new PVector(pg.x + inclinaison, 0); } } }