Initiation aux Shaders avec Processing
Le hello World des shaders
Les fichiers vert.glsl et frag.glsl sont à placer dans le dossier data du sketch.
shader_01
- vert.glsl
uniform mat4 transformMatrix; attribute vec4 position; attribute vec4 color; varying vec4 vertColor; void main() { gl_Position = transformMatrix * position; vertColor = color; }
- frag.glsl
#ifdef GL_ES precision mediump float; precision mediump int; #endif varying vec4 vertColor; void main() { gl_FragColor = vertColor; }
- shader_01.pde
PShader myShader; int margin = 32; void setup() { size(800, 600, P2D); myShader = loadShader("frag.glsl", "vert.glsl"); noStroke(); } void draw() { background(0); shader(myShader); fill(230, 120, 0); rect(margin, margin, width - 2*margin, height - 2*margin); resetShader(); // Désactive le shader, permet de redessiner normalement }
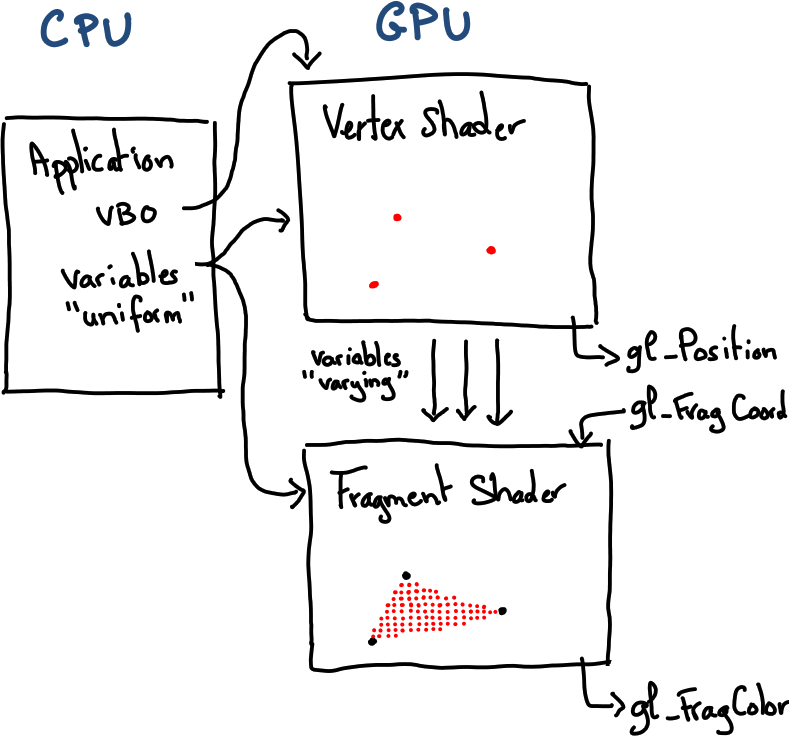
Communication entre l'application et les shaders
L'application (programme Processing) peut envoyer des données vers les shaders par des variable déclarées avec le mot-clé uniform.
Fonctions GLSL
- step(seuil, val)
Renvoi 0. si val < seuil, renvoi 1. si val > seuil
- smoothstep(seuil1, seuil2, val)
- clamp()
- pow()
- fract()
Returns the fractional part of a number
- mod(a, b)
a modulo b
- length()
- atan(y,x)
- mix(v1, v2, pct)
Interpolation linéaire entre v1 et v2 en fonction de 'pct'
- sign(float val)
Renvoi -1 si val est négatif, 1 si val est positif
Fonctions Processing pour transmettre des données
set(String name, int x) set(String name, int x, int y) -> vec2 set(String name, int x, int y, int z) -> vec3 set(String name, int x, int y, int z, int w) -> vec4 set(String name, float x, ...) set(String name, PVector vec) -> vec3 set(String name, int[] vec, int ncoords) // Jusqu'à 4 coordonnées par élément set(String name, float[] vec, int ncoords) set(String name, PMatrix2D mat) -> mat2 set(String name, PMatrix3D mat) -> mat4 set(String name, PImage tex) -> sampler2D
Attention ! Lorsqu'on transmet des nombres entiers, comme par exemple :set(“u_resolution”, 512, 512), soyez sûr d'avoir déclaré les variablesuniformpour des types entiers, comme :ivec2,ivec3…
Une autre solution est de les convertir en nombres flottants avant de les transmettre :set(“u_resolution”, float(512), float(512))
Variables uniform communes à tous les shaders dans Processing
Certaines variables uniform sont définies dans Processing et sont disponibles dans tous les shaders.
Elles sont déclarées dans le fichier PShader.java de Processing.
uniform mat4 transformMatrix; // la matrice de model view projection pour transformer les coordonnées du vertex du model space au clip space uniform mat4 projectionMatrix; // la matrice de projection permet de passer du camera space au clip space uniform mat4 modelviewMatrix; // la matrice modelview permet de passer du model space au world space puis au camera space uniform vec2 resolution; // contient la résolution de notre fenêtre uniform vec4 viewport; // contient la position de notre fenêtre ainsi que sa résolution
Textures
Pour sampler un texel en GLSL (extraire la couleur d'une texture à un point donné), on utilise la fonction:
texture2D(sampler2D image, vec2 uv)
Les coordonnes UV doivent être comprises entre 0.0 et 1.0
Elles pour origine le coin bas-gauche (0, 0) contrairement aux coordonnées d'écran, qui ont pour origine le coin haut-gauche.
Utilisation d'un buffer hors-écran
Pratique pour créer des effets avec retour d'information (feedback), comme par exemple un effet de réaction-diffusion.
PGraphics buffer = createGraphics(x, y, P2D); buffer.beginDraw(); buffer.shader(myShader); buffer.rect(0, 0, buffer.width, buffer.height); buffer.endDraw(); image(buffer, 0, 0);
Fonctions utiles
Couleur
Luminance
float luma(vec4 color) { return dot(color.rgb, vec3(0.299, 0.587, 0.114)); }
Brightness
float brightness(vec4 color) { return dot( color.rgb , vec3( 0.2126 , 0.7152 , 0.0722 )); }
HSB -> RGB
vec3 hsb2rgb( in vec3 c ){ vec3 rgb = clamp(abs(mod(c.x*6.0+vec3(0.0,4.0,2.0), 6.0)-3.0)-1.0, 0.0, 1.0 ); rgb = rgb*rgb*(3.0-2.0*rgb); return c.z * mix(vec3(1.0), rgb, c.y); }
RGB -> HSB
vec3 rgb2hsb( in vec3 c ){ vec4 K = vec4(0.0, -1.0 / 3.0, 2.0 / 3.0, -1.0); vec4 p = mix(vec4(c.bg, K.wz), vec4(c.gb, K.xy), step(c.b, c.g)); vec4 q = mix(vec4(p.xyw, c.r), vec4(c.r, p.yzx), step(p.x, c.r)); float d = q.x - min(q.w, q.y); float e = 1.0e-10; return vec3(abs(q.z + (q.w - q.y) / (6.0 * d + e)), d / (q.x + e), q.x); }
Random
float random2d(vec2 coord) { return fract(sin(dot(coord.xy, vec2(12.9898, 78.233))) * 43758.5453123); }
Noise
Gradient noise
// 2D Noise based on Morgan McGuire @morgan3d // https://www.shadertoy.com/view/4dS3Wd float noise (in vec2 coord) { vec2 i = floor(coord); vec2 f = fract(coord); // Four corners in 2D of a tile float a = random(i); float b = random(i + vec2(1.0, 0.0)); float c = random(i + vec2(0.0, 1.0)); float d = random(i + vec2(1.0, 1.0)); // Smooth Interpolation // Cubic Hermite Curve. Same as SmoothStep() vec2 u = f*f*(3.0-2.0*f); // u = smoothstep(0.,1.,f); // Mix 4 coorners percentages return mix(a, b, u.x) + (c - a)* u.y * (1.0 - u.x) + (d - b) * u.x * u.y; }
Fractional Brownian Motion
float hash(vec2 coord) { return fract(sin(dot(coord.xy, vec2(12.9898, 78.233))) * 43758.5453123); } float noise(vec2 U) { vec2 id = floor(U); U = fract(U); U *= U * ( 3. - 2. * U ); vec2 A = vec2( hash(id), hash(id + vec2(0,1)) ), B = vec2( hash(id + vec2(1,0)), hash(id + vec2(1,1)) ), C = mix( A, B, U.x); return mix( C.x, C.y, U.y ); } /** fBM stands for Fractional Brownian Motion https://iquilezles.org/articles/fbm/ Set octave to 8 for a detailed noise A value of 1.0 for H is good */ float fbm(vec2 x, float H, int octave) { float G = exp2(-H); float f = 1.0; float a = 1.0; float t = 0.0; for( int i=0; i<octave; i++ ) { t += a*noise(f*x); f *= 2.0; a *= G; } return t; }
Simplex noise
// // Description : GLSL 2D simplex noise function // Author : Ian McEwan, Ashima Arts // Maintainer : ijm // Lastmod : 20110822 (ijm) // License : // Copyright (C) 2011 Ashima Arts. All rights reserved. // Distributed under the MIT License. See LICENSE file. // https://github.com/ashima/webgl-noise // // Some useful functions vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; } vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; } vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); } float snoise(vec2 v) { // Precompute values for skewed triangular grid const vec4 C = vec4(0.211324865405187, // (3.0-sqrt(3.0))/6.0 0.366025403784439, // 0.5*(sqrt(3.0)-1.0) -0.577350269189626, // -1.0 + 2.0 * C.x 0.024390243902439); // 1.0 / 41.0 // First corner (x0) vec2 i = floor(v + dot(v, C.yy)); vec2 x0 = v - i + dot(i, C.xx); // Other two corners (x1, x2) vec2 i1 = vec2(0.0); i1 = (x0.x > x0.y)? vec2(1.0, 0.0):vec2(0.0, 1.0); vec2 x1 = x0.xy + C.xx - i1; vec2 x2 = x0.xy + C.zz; // Do some permutations to avoid // truncation effects in permutation i = mod289(i); vec3 p = permute( permute( i.y + vec3(0.0, i1.y, 1.0)) + i.x + vec3(0.0, i1.x, 1.0 )); vec3 m = max(0.5 - vec3( dot(x0,x0), dot(x1,x1), dot(x2,x2) ), 0.0); m = m*m ; m = m*m ; // Gradients: // 41 pts uniformly over a line, mapped onto a diamond // The ring size 17*17 = 289 is close to a multiple // of 41 (41*7 = 287) vec3 x = 2.0 * fract(p * C.www) - 1.0; vec3 h = abs(x) - 0.5; vec3 ox = floor(x + 0.5); vec3 a0 = x - ox; // Normalise gradients implicitly by scaling m // Approximation of: m *= inversesqrt(a0*a0 + h*h); m *= 1.79284291400159 - 0.85373472095314 * (a0*a0+h*h); // Compute final noise value at P vec3 g = vec3(0.0); g.x = a0.x * x0.x + h.x * x0.y; g.yz = a0.yz * vec2(x1.x,x2.x) + h.yz * vec2(x1.y,x2.y); return 130.0 * dot(m, g); }
Rotations
2D
mat2 rotation2d(float a) { float c=cos(a); float s=sin(a); return mat2(c,-s,s,c); } vec2 rotate(vec2 v, float angle) { return rotation2d(angle) * v; }
3D
mat4 rotation3d(vec3 axis, float angle) { axis = normalize(axis); float s = sin(angle); float c = cos(angle); float oc = 1.0 - c; return mat4( oc * axis.x * axis.x + c, oc * axis.x * axis.y - axis.z * s, oc * axis.z * axis.x + axis.y * s, 0.0, oc * axis.x * axis.y + axis.z * s, oc * axis.y * axis.y + c, oc * axis.y * axis.z - axis.x * s, 0.0, oc * axis.z * axis.x - axis.y * s, oc * axis.y * axis.z + axis.x * s, oc * axis.z * axis.z + c, 0.0, 0.0, 0.0, 0.0, 1.0 ); } vec3 rotate(vec3 v, vec3 axis, float angle) { return (rotation3d(axis, angle) * vec4(v, 1.0)).xyz; }
Flou Gaussien
Code optimisé, d'après https://www.rastergrid.com/blog/2010/09/efficient-gaussian-blur-with-linear-sampling/
A exécuter en deux passes : horizontale et verticale
vec4 blur(sampler2D image, vec2 uv, vec2 resolution, vec2 direction) { const float offset[3] = float[](0.0, 1.3846153846, 3.2307692308); const float weight[3] = float[](0.2270270270, 0.3162162162, 0.0702702703); vec4 colorOut = texture2D(image, uv / resolution) * weight[0]; for (int i=1; i<3; i++) { vec3 color = texture2D(image, (uv + direction * offset[i]) / resolution); color += texture2D(image, (uv - direction * offset[i]) / resolution); colorOut += color * weight[i]; } return colorOut; }
Librairies Processing
Quelques librairies externes pour l'utilisation de shaders dans Processing :
Ressources
Liste de liens incontournables pour approfondir et aller plus loin…